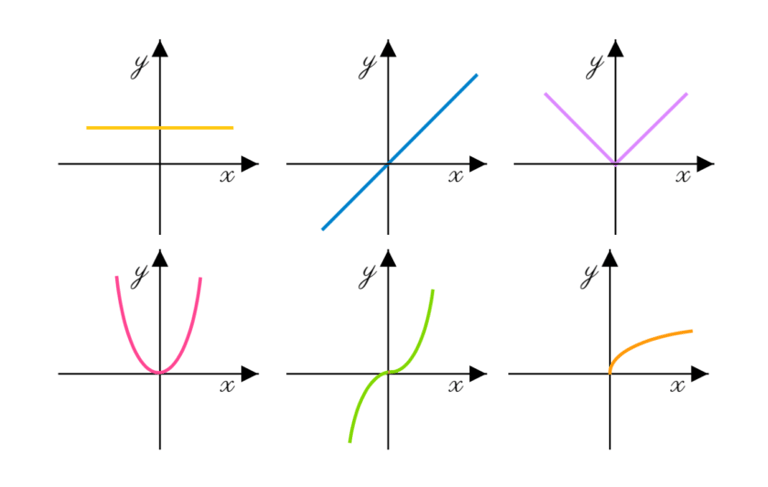Números e Álgebra
Em construção... aguarde.
Naturais
Os números naturais (N) são o primeiro conjunto numérico com que temos contato, usados instintivamente para contar e ordenar. Eles formam a base fundamental de toda a matemática, servindo como alicerce para a construção de conjuntos mais complexos. Suas operações de adição e multiplicação são os pilares de toda a aritmética que conhecemos.
Atividade:
Inteiros
O conjunto dos números inteiros (Z) expande os naturais ao incluir seus opostos negativos além do zero. Essa expansão foi crucial para representar perdas, dívidas, temperaturas abaixo de zero e direções opostas. Eles nos permitem trabalhar com a noção de dualidade, tornando a matemática capaz de descrever situações do mundo real com muito mais precisão e abrangência.
Atividade:
Racionais e Irracionais
Os números racionais (Q) são todos aqueles que podem ser escritos como uma fração, incluindo finitos e dízimas periódicas. Já os irracionais (I) são o oposto: números com infinitas casas decimais que nunca se repetem, como o famoso π (Pi) e a raiz de 2 . Juntos, esses dois conjuntos preenchem completamente a reta numérica, formando o universo dos números reais.
Atividade:
Reais
O conjunto dos números reais (R) representa a união de todos os números racionais e irracionais. Ele preenche de forma contínua e sem lacunas toda a reta numérica, incluindo desde os inteiros até números como π e raiz de 2. É o conjunto fundamental para medir grandezas contínuas como distância, tempo e temperatura, servindo como a base para o cálculo e a maior parte das ciências exatas.
Atividade:
Relações entre conjuntos
As relações entre conjuntos estudam como eles interagem. As noções básicas são a pertinência (um elemento pertence a um conjunto) e a inclusão (um conjunto está contido em outro). A partir disso, operações como união, interseção e diferença nos permitem combinar e filtrar grupos. Essa lógica é a base da organização de dados, da programação e do raciocínio categórico em todas as áreas.
Atividade:
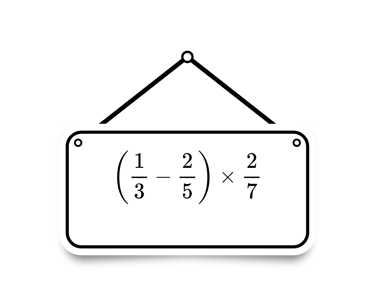
Expressões
Expressões matemáticas são combinações de números, variáveis e operações que representam um valor. Funcionam como frases na linguagem da matemática, formulando um cálculo a ser resolvido, mas sem uma igualdade. Elas podem ser numéricas (apenas números) ou algébricas (com letras). Dominá-las é o primeiro passo para construir equações e modelar situações do mundo real de forma lógica.
Atividade:
Equações e Inequações
Equações são sentenças matemáticas que estabelecem uma igualdade (=) entre duas expressões, buscando um ou mais valores específicos que a tornem verdadeira. Já as inequações trabalham com desigualdades (<, >, ≤, ≥), comparando expressões para encontrar um conjunto ou intervalo de soluções. Enquanto equações buscam um ponto de equilíbrio, inequações definem limites e restrições.
Atividade:
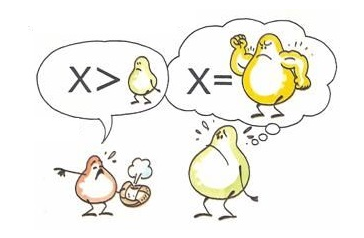
Sequências
Uma sequência é um conjunto de elementos dispostos em uma ordem específica. Cada elemento é chamado de termo e sua posição é crucial. Elas podem ser finitas ou infinitas e frequentemente seguem uma lei de formação, como nas progressões aritméticas (PA) e geométricas (PG). Sequências são essenciais para estudar padrões, o crescimento de populações e o comportamento de mercados financeiros.
Atividade:
Função
Função é uma das ideias mais centrais da matemática, descrevendo uma regra que relaciona cada elemento de um conjunto de entrada (domínio) a um único elemento de um conjunto de saída (contradomínio). Ela modela a dependência entre duas grandezas variáveis. As funções são a base para descrever fenômenos, prever resultados e construir gráficos em todas as áreas da ciência e tecnologia.
Atividade:
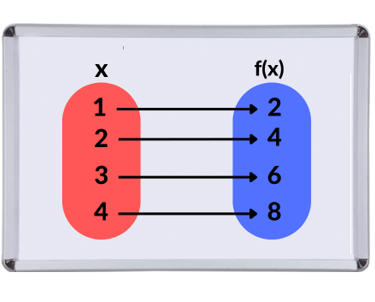
Tipos de Função
As funções são classificadas conforme sua lei de formação. As mais comuns incluem a função afim, cujo gráfico é uma reta e descreve taxas constantes. A quadrática gera uma parábola, modelando trajetórias. Já as funções exponencial e logarítmica são cruciais para descrever crescimentos acelerados e fenômenos de escala.
Atividade:
"A educação não transforma o mundo. A educação muda as pessoas. Pessoas transformam o mundo."
Paulo Freire
